Computing Cryptographic Hashes for Cyclic Dependencies

"Much more than encryption algorithms, one-way hash functions are the workhorses of modern cryptography." —Bruce Schneier

Cryptographic hashes (or one-way hash functions) allow us to compute a digest that uniquely identifies a resource. If we make a small change anywhere in a resource, its digest also changes—drastically, because of the Avalanche effect.

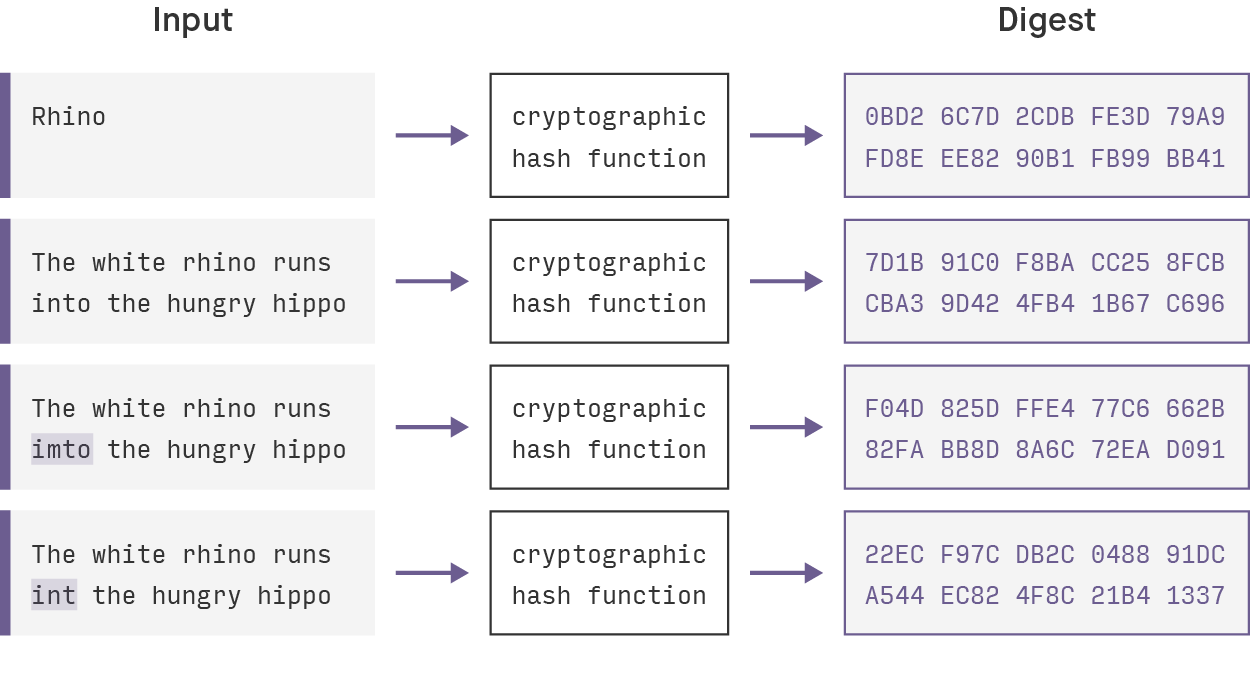
This characteristic makes the hashes very practical for detecting changes in applications that deal with dependency trees. If we include the cryptographic hashes of the dependencies of a resource in the resource's own cryptographic hash, we have a cheap way to check if a resource or any of its dependencies were changed. This pattern is commonly used in the software world. For example, think of git hashes, blockchains, and the nix build system.

Implementation is theoretically not that hard, given a good cryptographic library. However, it gets trickier when we want to allow dependency cycles. At that point, we get a bit of a chicken-and-egg problem: we need resource A’s hash to compute resource B’s hash, but that in turn depends on B’s hash again!

Cyclic Cloud Resources

Let's start by giving a more concrete example of how we encountered this problem. In Fugue, we are dealing with constructing complicated cloud infrastructure. Cyclic dependencies between resources inevitably pop up once in awhile.

For example, it’s not uncommon to have two Security Groups that refer to each other. Imagine you have a default security group, which contains the core of your application, and a monitoring security group which performs health checks. Two considerations are key:

• You want to allow traffic from monitoring to default in order to perform external sanity checks;

• You also want to allow traffic from default to monitoring in order to perform heartbeat-like checks or to have your application send detailed information.

Configuring these in mainstream configuration languages often leads to annoying cyclic dependency issues, which in turn require annoying and verbose workarounds. In Fugue, we use a statically typed, declarative programming language called Ludwig to configure infrastructure. This allows us to solve the problem in a neat way.

In this blog post, we’ll study how we can solve part of the problem—detecting changes in these possibly cyclic dependency graphs.

Literate Haskell

It’s useful to step back for a quick moment and make sure you’ll have easy access to the logic and code involved in our study. This blogpost is written in Literate Haskell, which is an implementation of literate programming for the Haskell programming language. The term, literate programming, was coined in the early 1980s by Dr. Donald Knuth, who cited CWEB as his favorite programming language.

In literate programming, we communicate an idea by presenting a human-readable text interspersed with snippets of code. This is the reverse of "normal" programming, where we intersperse our code with comment snippets.

It’s perfect for technical blog posts … and, of course, we really like Haskell.

As a result, you can compile this blog post easily with a Haskell compiler, or even better, load it into the GHCi REPL and play around with it. In order to do that, download the code to this blog post and load it in GHCi:

$ ghci cyclic-hash.lhsGHCi, 
version 7.10.3: http://www.haskell.org/ghc/ :
? for help[1 of 1] 
Compiling Data.CyclicHash ( cyclic-hash.lhs, interpreted )Ok,
 modules loaded: Data.CyclicHash.*Data.CyclicHash

In order for the blog post to work as a standalone Haskell module, we need to do some setup first. We start with a reasonably standard Haskell module header and declare the language pragmas that we need:

{-# LANGUAGE BangPatterns #-}
 {-# LANGUAGE FlexibleContexts #-} 
{-# LANGUAGE GADTs #-} 
{-# LANGUAGE MultiParamTypeClasses #-} 
{-# LANGUAGE TypeFamilies #-}

Then, we describe the exported interface of this module. Following good technical design standards, we try to keep this to a minimum:

module Data.CyclicHash ( CyclicHash (..) , HashField (..) , cyclicHashes ) where

Lastly, we have to import a number of other modules we rely on. Most of these modules ship with the base library provided by the compiler, and the others are provided by three very commonly used libraries: containers, hashable, and unordered-containers.

import Control.Monad (forM_) 
import Data.Hashable (Hashable, hashWithSalt) 
import Data.List (foldl') 
import Data.Maybe (fromMaybe, maybeToList) 
import Text.Printf (printf) 
import qualified Data.Graph as G 
import qualified Data.HashMap.Strict as HMS

Problem Definition

The simple example of cyclic dependencies that we’ll explore can be modeled in a trust graph. We want to compute cryptographic hashes for all the people in this trust graph. Because trust can be mutual, we quickly encounter the problem of dependency cycles here.

Let's look at the data type we will use to model our problem:

type Username = Stringdata Person = Person { 
pUserName :: Username,
pFullName :: String,
pTrusts :: [Username] 
} deriving (Show)

A Person has a Username, which we will use as a key, and a full name. A Person also has a list of other people he or she trusts. The cryptographic hash of a Person consists of the username, the full name, and the hashes of the people this person trusts.

The CyclicHash Class

We start out with a class that captures the essence of computing hashes for cyclic data structures.

We need an associated type synonym, Key, which gives us a unique key for the value. We also have a corresponding key function to obtain this key.

Usually the hash of a data type is a hash of all the fields in that data structure. This is why we have the second important function, fields. It returns a list of all the fields we want to hash:

class (Hashable (Key a), Ord (Key a)) = CyclicHash a 
where type Key a 
key :: a - Key a 
fields :: a - [HashField a]

The fields we want to hash are represented using an intermediate data type.

We make a distinction between two kinds of fields:

• Primitive fields (Int, String, and other things that have a reasonable Hashable instance). These just contain the value that needs to be hashed.

• Dependency fields which refer to other values. These are the ones we need to be careful about, since they can introduce dependency cycles.

Note:

data HashField a 
where PrimitiveField :: Hashable 
b = b - HashField a 
DependencyField :: Key a - HashField a

We can now write down the CyclicHash instance for Person. It is fairly straightforward: pUserName and pFullName contribute to the hash as primitive fields, and we create a DependencyField for every person in pTrusts:

instance CyclicHash Person 
where type Key Person = Username 
key p = pUserName p 
fields p = [ PrimitiveField (pUserName p), PrimitiveField (pFullName p)] ++
map DependencyField (pTrusts p)

Lastly, let's add an auxiliary method that gives us simply the dependencies of a node. We can do this by finding all the DependencyField fields and concatenating their keys in a list:

dependencies :: 
CyclicHash a = a - [Key a]dependencies node = [k | DependencyField k - fields node]

Aside: The Hashable Library

In this blogpost, we use the hashable library because of its easy interface and wide adoption. However, we must keep in mind that this library does not provide us with cryptographically strong hash functions.

In production code, it would be better to use an algorithm like SHA-2. The idea behind the cyclic hashing stays the same though, so updating this code to use such an algorithm is not a hard task.

A Primitive Hash

We can start by defining a "primitive" hash function, which does not look at the dependencies of a node:

primitiveHash :: 
CyclicHash a = Int - a - IntprimitiveHash 
salt = foldl' hashField salt . fields 
where hashField s (PrimitiveField x) = s `hashWithSalt` (0 :: Int) `hashWithSalt` x 
hashField s (DependencyField k) = s `hashWithSalt` (1 :: Int) `hashWithSalt` k

A Component Hash

Now, we want some way to take the hashes of the dependencies into account. But that is impossible to do if we have a trust graph like this:

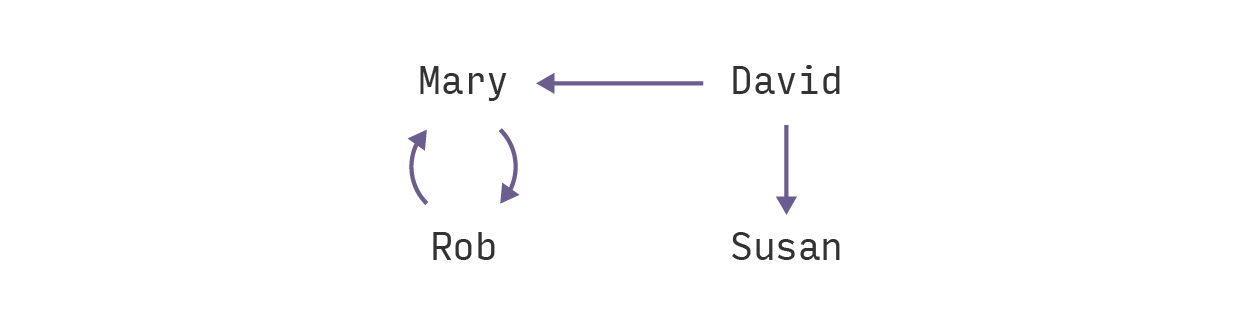
In Haskell, this looks like:

_people :: [Person]_people = [ Person "rob" 
"Robert Smith" ["mary"] ,
Person "mary" "Mary Johnson" ["rob"] ,
Person "susan" "Susan Williams" [] ,
Person "david" "David Brown" ["mary", "susan"] ]

Mary's hash depends on Rob's hash and vice versa! An elegant way to solve this is provided to us by computing the strongly connected components of the graph.

We will be able to compute the strongly connected components using the vastly underrated Data.Graph module. The output for the example graph we saw above is:

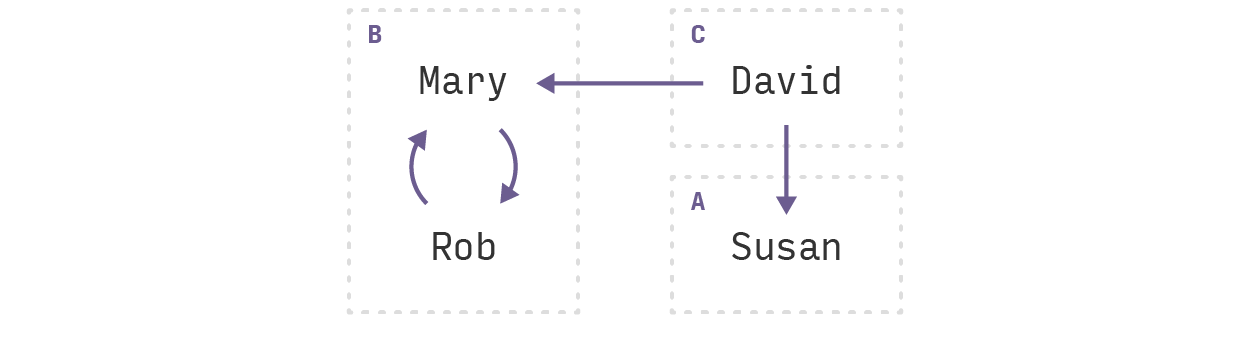
A very important property of the resulting components is that, if we look at the graph of components, there cannot be any cycles. This is easy to see; if there were a cycle between two or more components, they would belong to the same cyclic component!

Now, we can compute a hash per component. The simplest strongly connected component is a single vertex (represented by the G.AcyclicSCC constructor). In this case, we can rely on the primitiveHash function we saw above. Otherwise, we have a list of vertices (G.CyclicSCC). We can hash these together by using a fold.

Note that this hash also contains the shape of the component:

componentHash ::
CyclicHash a = Int - G.SCC a - IntcomponentHash 
salt0 (G.AcyclicSCC x) = salt0 `hashWithSalt` (0 :: Int) `primitiveHash` xcomponentHash 
salt0 (G.CyclicSCC xs0) = salt0 `hashWithSalt` (1 :: Int) `hashPrimitives` xs0 
where -- | Chain of primitiveHash. hashPrimitives salt = foldl' primitiveHash salt

This gives us something like the following for our example; we use <+> as an informal operator to denote a combination of hashes:

componentHash(A) = 0 + primitiveHash(susan)componentHash(B) = 1 + primitiveHash(rob) + primitiveHash(mary)
componentHash(C) = 0 + primitiveHash(david)

Note that the <+> operator is not commutative, so the order in which we do the fold is important. Fortunately, the Data.Graph library takes care of that for us. The nodes returned in a component are sorted in the order we need.

A Component Hash Per Node

With the help of the componentHash function, we can define another function which gives us the map containing the hash for each component, by node:

componentHashes :: CyclicHash a = Int - [G.SCC a] - HMS.HashMap (Key a) 
IntcomponentHashes salt sccs = HMS.fromList $ do scc - sccs 
let !hash = componentHash salt scc 
node - G.flattenSCC scc 
return (key node, hash)

For the example graph, this gives us the following mapping:

rob = componentHash(B)david = componentHash(C)susan = componentHash(A)mary = componentHash(B)

The Cyclic Hash

Now, we have almost all the ingredients to compute the full cyclic hash for a value. What we want to do is easy to informally define, but a bit harder to implement.

Since we know there are no cyclic dependencies between the strongly connected components of the graph, we can run through them in order now.

1. Let's start with component A which is the simplest. Since the nodes in this component have no dependencies whatsoever, we get:

cyclicHash(susan) = primitiveHash(susan)

2. For component B, it's a bit more complicated. Ideally, we would have something like this, which is of course impossible:

cyclicHash(rob) = primitiveHash(rob) + cyclicHash(mary)cyclicHash(mary) = primitiveHash(mary) + cyclicHash(rob)

But we can fix this by, instead of taking the cyclic hashes of nodes in the same component, taking the component hashes, since these hashes also contain the whole component! This gives us:

cyclicHash(rob) = primitiveHash(rob) + componentHash(B)cyclicHash(mary) = primitiveHash(mary) + componentHash(B)

3. When we arrive at component C, we have already computed the cyclic hashes of its dependencies, so we simply get:

cyclicHash(david) = primitiveHash(david) + cyclicHash(mary) + cyclicHash(susan)

The implementation of cyclicHash is similar to primitiveHash, except we now pass in an argument dependencyHashes. The idea is that this will contain the cyclicHashes of actual dependencies and the componentHashes of cyclic dependencies (which are in the same component). Fortunately, we don't really need to check which of these cases we are in—we can just grab the hash from the map:

cyclicHash :: CyclicHash a = HMS.HashMap (Key a) 
Int - Int - a - IntcyclicHash dependencyHashes salt0 = foldl' hashField salt0 . fields 
where hashField !s (PrimitiveField x) = s `hashWithSalt` (0 :: Int) 
`hashWithSalt` x hashField !s (DependencyField k) = let !x = fromMaybe 0 $ HMS.lookup 
k dependencyHashes in s `hashWithSalt` (1 :: Int) `hashWithSalt` x

Tying It All Together

Finally, it's time to put everything together in a single function that users can call. In fact, this is the only top-level function exported from this module!

The function takes a number of values and returns the values paired with their hashes. Of course, the interesting bit is how we construct fullHashes:

cyclicHashes :: CyclicHash a = Int - [a] - [(a, Int)]cyclicHashes salt0 nodes = [ (n, h) | n - nodes , h - maybeToList 
$ HMS.lookup (key n) fullHashes ]

We start off by calculating the strongly connected components using the Data.Graph library. Then, we calculate a hash for every component, using the componentHashes we defined before:

  where    comps      = G.stronglyConnComp [(n, key n, dependencies n) | n <- nodes]    compHashes = componentHashes salt0 comps

It is important to note that G.stronglyConnComp returns the components in topological order. For our use case, this means that the components are in the "right" order with regards to dependencies: if y depends on x, x will always be placed before y in the list.

As a result, we can just fold through the comps components. The accumulator we use is the map we calculated using componentHashes. Initially, this map contains the componentHash for every node, but as we fold through the list, we update it to contain the full hash for every node. This is exactly what cyclicHash expects!

 fullHashes = foldl'(acc scc - let !newHashes = HMS.fromList [ (key x, cyclicHash acc salt0 x) | x - G.flattenSCC scc ] in HMS.union newHashes acc) compHashes comps

Full Example Code

Let's add a quick printing function to check the results:

_printCyclicHashes :: (CyclicHash a, Show (Key a)) = [a] - IO ()_printCyclicHashes values = forM_ (cyclicHashes 42 values) $ (x, hash) - printf "%s: %xn" (show (key x)) hash

*Data.CyclicHash _printCyclicHashes _people"rob": 9923cc533bb3432"mary": e8c6608ddd959521"susan": 6dd70fb3a3e127ed"david": 86b49a12d999cc35

Then, after we edit, for example, mary's name, we get:

*Data.CyclicHash _printCyclicHashes _people"rob": 201403e3ca292874"mary": 8370448e0b8598cf"susan": 6dd70fb3a3e127ed"david": 853624228d76fe7f

Seems like it is behaving as expected!

It goes without saying that algorithms like this need more rigorous testing, but the concept holds up to initial scrutiny.